|
▼ 最小二乗推定量の導出
最小2乗推定量(残差平方和を最小にする公式)
微分を利用して、上式の導出を行う。
最小二乗法は、観測値の平均からの平方偏差の和を最小にすることで、いまその和をS2とすると次のように書ける。
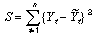
または
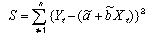
で与えられる。和S2を最小にする変数a,bの組み合わせを決定するには、S2を変数a,bに関して偏微分する。
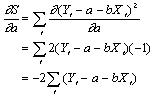
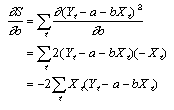
上の2式の導関数を0とおき、a,bの推定量を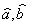 とおくと とおくと
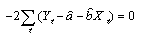 (式1 ) (式1 )
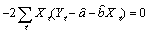 (式2 ) (式2 )
を得る。推定量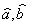 として残差etを考慮すると として残差etを考慮すると
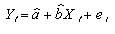
と書くことができる。このとき残差を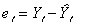 と示すことができる。 と示すことができる。
以上のことから、最小二乗法は「残差の二乗和」を最小にするようにパラメータa,bを推定する方法と考えることができる。式(1),式(2)は次のように書き表せる。
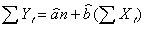 (式3 ) (式3 )
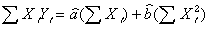 (式4 ) (式4 )
式(3),式(4)は「最小二乗正規方程式」と呼ばれている。また
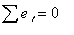 (式5 ) (式5 )
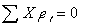 (式6 ) (式6 )
となる。(式(5),式(6)となることを確かめよ。(Hint! 式(1),式(2)の括弧の中を考えよ。)
式(3),式(4)を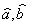 について解く。 について解く。 の解は の解は
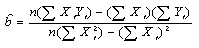 (式7 ) (式7 )
となり、式(7)の分子について考えてみると、
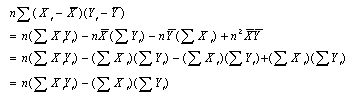
となる。ここに
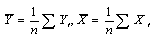
また、(7)の分母は次のように書き表せる。
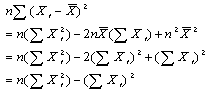
上のことから式(7)は次のように書ける。
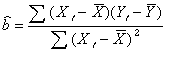 (式8 ) (式8 )
いま、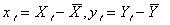 とおきかえると、 とおきかえると、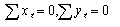 であるので、式(8)は であるので、式(8)は
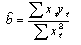
と書き表せる。の解は、式(3)からただちに求めることができる。
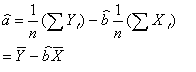 (式10) (式10)
以上のことから標本回帰式は次のように表わされる。
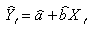
| □例題:正規方程式の条件 |
難易度:★★★ |
目安時間:20分 |
|
|
正規方程式の条件であるXeの合計を計算してみよ。正規方程式の条件を満たしているかを確認せよ。
|
|
|
last modified :2005.11.05
|