真のモデルは神のみぞ知るところであり、神が意地悪でなければ、データは最も出現しやすい値を神様が与えて下さったと考えることができる。神の意志に背かないよう、もっとも出現しやすいようなパラメータの値を選べば、真のパラメータに近い値を得ることができるであろう。
生起確率密度関数の積を尤度関数と定義し、この尤度関数を最大にする考え方を応用して尤も出現するようなパラメータの推定を行う。いま、正規分布を仮定すれば、正規分布の確率密度関数をかけ合わせたものを尤度として以下のように表す。
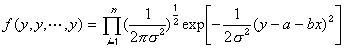
尤度(L)を最大にするようにパラメータa, b, を選ぶのだから、積の形では計算が面倒なので、以下のように尤度関数の両辺を対数をとる。(対数尤度)
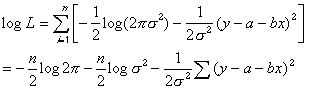
この関数を最大にするには、第3項を最小にすればよい。よって最小2乗推定量を求めることと同じ手続きになる。これを解けば、データ数が大きくなると最尤法の推定値と最小2乗推定値は同じになる。(もちろんデータの分布を他の分布とすれば、確率密度関数が違うので推定量は異なる。)