▼ 母集団と標本の関係
これまで回帰モデルの「推定」作業を行ってきたが、推定結果であるパラメータの値が本当に真のモデルからえられたものであるというチェックが必要である。真のモデルからではなく、他の母集団から得られたデータであるという過ちを排除するために統計的検定の手法を用いる。
「検定」とはパラメータの値に関する仮説検定を行う手続きである。(ここで実際には母集団の分布状態もわからない場合が多いが、ここでは正規分布をすると仮定し、既に母集団分布だけはわかっているので、パラメータの値についてのみ仮説検定を行うというものである。)
いままで展開してきたように、母集団についてY = a + b X + uという回帰モデルを想定し、標本観察データを用いてY = a + b X + uというパラメータの値を推定し、標本回帰式を求めた。得られた標本が、真の母集団か他の母集団から得られたのかどうかは明確でない。真の母集団から任意に得られたと想定したが、他の母集団から得られた標本とみなす方がよいかもしれない。得られた一部の標本観察値を用いて、真の母集団で想定したような回帰モデル:Y = a + b X + uという関係がはたして存在するのかどうか、b=0のような回帰関係が存在するのかどうか、を明確にすることが、パラメータの値に関する仮説検定という。これらのことが明確でないと標本観察値を用いてa,bの推定値を求めても意味がないことになる。つまり仮説検定では、確かに真の母集団で想定した回帰モデルから得られた標本である(すなわち他の母集団から得られた標本でない)ということを明確にする作業である。
■ 母集団と標本の関係
| 母集団 |
データ(標本) |
| 母平均:μ (未知)
母分散:σ2 (未知)
|
データ(標本)平均: 既知:推定値) 既知:推定値)
データ(標本)分散: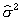 既知:推定値) 既知:推定値)
|
| 母集団 |
データ(標本) |
| 母パラメータ:b (未知)
誤差項:u (未知)
|
標本パラメータ: (既知:推定値) (既知:推定値)
残差項:e (既知:推定値)
データ(標本)分散: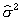 (既知:推定値) (既知:推定値)
|
t検定:標本の数が少ないときに用いられる
F検定:
カイ2乗検定:度数分布の適合度検定方法
統計関数から各数値表を作る。
| □例題:●●●●●●● |
難易度:★★★★ |
目安時間:●分 |
例題集 |
|
|
|
|
last modified :2005.09.01
|