▼ 予測誤差と信頼限界
■
| □例題:●●●●●●● |
難易度:★★★★ |
目安時間:●分 |
例題集 |
|
|
|
|
検定で行った方法の応用として、Xを与えたときのYの値の予測に関する信頼限界を求める。すなわち、確率変数aとbによって導出された (推定値)もまた確率変数なので、その散らばり具合をグラフ上に示すことから信頼区間を示すことができる。いま実際のデータ以外のX, Y(ここでは、予測値)をX0,Y0とする。X0を与えるとYの予測値Y0は (推定値)もまた確率変数なので、その散らばり具合をグラフ上に示すことから信頼区間を示すことができる。いま実際のデータ以外のX, Y(ここでは、予測値)をX0,Y0とする。X0を与えるとYの予測値Y0は
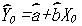
となる。Y0の真の値は、Y0=a+bX0+u0であるから
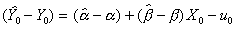 (式1) (式1)
と書き表すことができる。両辺に期待値をとると、abともに不偏推定量であるから、右辺の第1,2項は0となる。また誤差項の仮定から第3項も0となることは明らかである。左辺(予測量)はとなり、不偏推定量であることが確認された。
次に、予測誤差の散らばり具合を見るために分散を考える。式(1)の両辺の分散をとる。
 (式2) (式2)
散らばり具合(95%信頼区間:検定では5%有意水準)を求め、表に書くことができる。分散はaとbの計算の基になった観測値の平均である から遠く離れるに従って大きくなることが式からもわかる。以下の例題にて上記のことを確認せよ。 から遠く離れるに従って大きくなることが式からもわかる。以下の例題にて上記のことを確認せよ。
| □例題:予測 |
難易度:★★★ |
目安時間:20分 |
例題集 |
|
例題3-5をもとに式2を使って、Xの予測値の95%信頼区間を求めそれを図示せよ。なお、Xデータの範囲内にある予測を標本内予測と呼び、データの両端より外側での予測を標本外予測という。この図をプリントアウトし、標本外予測の範囲を示せ。(印刷の際には、ヘッダーに名前を入れること。)
|
|
|
last modified :2003.09.27
|