|
▼ t分布
■ t分布の形状
t分布(t-distribution)は母集団の分散が未知である場合に、平均に関する仮説を検定する際に使える。回帰分析のパラメータは、確率変数であるから平均や分散を持つ。しかし、母集団の分散はわからないので、これらの平均値(推定値)を検定するのにはt検定が使われる。
t分布の形は、標準正規分布(平均:0、分散:1)に似て原点に対し左右対称で、データ数(自由度)が多くなればなるほど標準正規分布の形状に近くなる。図でわかるようにt分布の方が裾が厚くなっている。
■ WEBコンポーネントによるt分布の形状
3年生以下のノートPCで利用可能
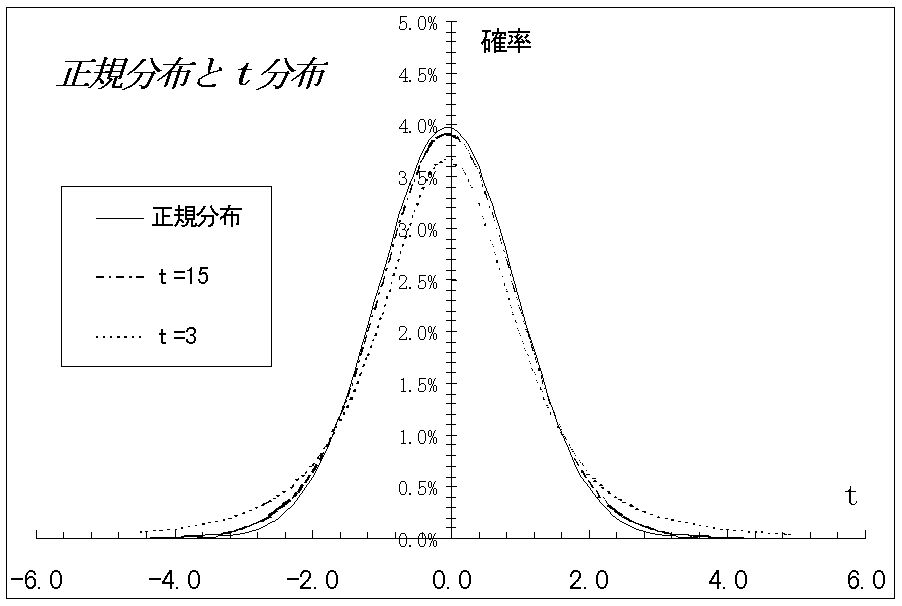
図 t分布と正規分布(クリックすると大きくなります)
| □例題:t分布とt値 |
難易度:★ |
目安時間:10分 |
データ |
| 曲線の下の部分とX軸に囲まれた部分の面積はいくつか?上の拡大図をプリントアウトしt値が1のときの位置とその確率を示しなさい。また、1以上である確率を示しなさい。 |
| ヒント:tが1以上である確率は面積に相当することに注意する。 |
自由度と決めるとそれに応じたt分布の形状が決定される。その分布に従って各値ごとの確率密度を決定する(横軸x:t値、縦軸y:確率密度)。図の山の頂上のt値は0である。
ここでの関数は
y = f(x,自由度) (式1)
となる。
| □例題:t分布の形状 |
難易度:★★★★ |
目安時間:50分 |
データ |
式1を利用して上図ようなt分布の形状を描きなさい(自由度は3と15)。ここでは、横軸Xに相当する高さ(y)を求めるような関数を利用する。
- 横軸であるXを0.1きざみで-6〜6まで作成
-
-
|
| Hint !
Excelには、t分布の累積確率密度を求める標準関数(=tdist)があるので、TDIST関数を使って累積確率密度を求める。次にこれらを使って各値ごとの生起確率を求める。度数分布表を作ったことを思い出せばよい。 |
■ t分布の数値表
統計学のテキストの巻末付録として、様々な分布関数の数値表が掲載されている場合が多い。t分布の数値表は必ずといってよいほど掲載されているが、これは確率と自由度でそれに対応する臨界値が決まるというものである。。Excelの標準関数のTINV関数(t分布の逆関数)を使って数値表を作成することができる。
| □例題:t分布の数値表 |
難易度:★★ |
目安時間:25分 |
データ |
| t分布の数値表を作成せよ。確率は下記の通りで、自由度は20までとる。 |
t値 数値表 t = f(確率 ,自由度)
| 自由度/確率 |
0.1 |
0.08 |
0.06 |
0.04 |
| 1 |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
| 2 |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
| 3 |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
| ... |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
=TINV(セル,セル) |
作成後に、この表はどのように用いるかを考えよ。
■ t値の意味と合格基準
もしt値が1であった場合、真の値が0であるという(すなわちパラメータを推定する意味がない)確率は非常に高くなる。逆に、t値が15というような頂上からかなり遠い位置にあれば、この推定値は0である可能性はほとんどなくなる。(しかし、何百回に一度ぐらいの程度で0が生ずる可能性はまだ残されている。)このようなt値を用いて判断することで客観的に推定値は0ではないことがある程度保証される尺度が作成できる。
では、何パーセントの割合で生ずれば0でないと判断してよいのだろうか。これは「東京は富士山の麓(付近)にある」といえるかという質問に類似している。「箱根は富士山の麓にある」ことは皆が認めるであろうが、前者を認める人は少ないはずである。仮に富士山の周辺の高度150m以上を富士山の麓とするといった適当な基準を決めて判断すれば、その地域を限定できる。
同様に平均0であるかどうかを判断するのに、裾野の面積はt分布において生ずる確率とみなせるので、0となる確率を5%(有意水準)未満という基準を使用することで係数を0とみなすかどうかの線を引く。5%有意水準とすれば、20回に1回の割合で起こる確率ということであり、有意水準1%、あるいは5%とするかどうかは分析者の判断による。通常の回帰分析では、t値は少なくとも2以上は要求される。
注意:t値が大きいことは,その変数の説明力が大きいということにはならないので注意すること。
■ 有意水準:合否の基準
例えば、テストにおいて85点をとったとする。その成績で合格するかどうかはテストを実施する方が決める。この場合に、合格基準が80点であれば合格となるが、厳しい基準90点となると不合格になってしまう。
今、b=0であることをチェック(テスト)するため、その基準を決める。この基準を確率を用いて表したものが有意水準(significance level)である。1/20で生じる基準を有意水準5%、1/100で生じる基準を有意水準1%という。厳しい基準で合格した方が、信頼性は増すが、その基準はt値表によって決められる。
| □例題:有意水準 |
難易度:★★ |
目安時間:15分 |
データ |
| 有意水準を5%と1%とした場合に、例題のt値と比べることから、これらのパラメータの値が0(b=0)である仮説を棄却できるかどうかを考えよ。(合格は、b=0が棄却、否定できることである。) |
判定基準
| 基準
| 有意水準
| 生起確率
| 合否/採択or棄却
|
| 基準1(厳しい)
| 0.5%
| 1/200
|
|
| 基準2
| 1%
| 1/100
|
|
| 基準3
| 3%
| 3/100
|
|
| 基準4(緩い)
| 5%
| 1/20
|
|
■ p値
t値に代わりp値(p-value)という統計量も使われる。p値とは、パラメータのt値から計算した累積密度である。この統計量を用いるメリットは、有意水準に対して合否を決定するするのでなく試験者がその値から直接判断できる点である。
例えば、自由度15でパラメータのt値が3であるとすると、t値表から5%や1%で合格しているかどうかを調査をしなくてはならないが、p値ならばその値から13.4%の確率で生ずるというように判断できるので、合格基準と比較する作業は不要となる。
なお、Excelの分析ツールにある回帰分析では、t値だけでなくp値も出力される。
■ t分布をする統計量
Y = a + bX + u の推定時に誤差項uに関する仮定が必要となる。例えば、標本平均μ、分散σ2の正規分布に従う母集団から得られたn個のデータをx1, x2, ・・・xn とするとき、次の式で与えられるTは自由度n-1のt分布に従う。(証明略)
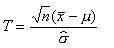 (式1) (式1)
ここで、式1を変形して計算しやすい形(式2、式3)に改める。
■ 有意性検定:t検定
もし推定した係数がゼロ(b=0)であったならばどうであろうか。このようなケースではパラメータの推定の意味そのものがおかしい。すなわち,その説明変数は何も説明していないことと同じである。ここでは、パラメータの有意性(すなわち、パラメータの値がゼロでないこと)を確かめるために各係数に対しt検定を行う。
ここで、t検定を行うときに誤差項に関する仮定が必要となる。
仮定: 撹乱項 u1, u2,・・・ ut は相互に、平均0,分散σ2の正規分布に従う。
例えば、標本平均のt検定をする場合では、平均μ、分散σ2の正規分布に従う母集団から得られたn個のデータをx1, x2, ・・・xn とするとき、次の式で与えられるtは自由度n-1のt分布に従う。(証明略)
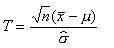 (式1) (式1)
(ただし、 はデータの平均、 はデータの平均、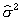 はデータの分散。)この式は、基準(正規)化の式に類似している。(どの変数が異なっているかを考えよ。)この分布の形状をもとに判定をする。この分布の詳細については次の項を参照せよ。 はデータの分散。)この式は、基準(正規)化の式に類似している。(どの変数が異なっているかを考えよ。)この分布の形状をもとに判定をする。この分布の詳細については次の項を参照せよ。
last modified :2005.09.07
|

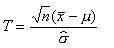 (式1)
(式1) はデータの平均、
はデータの平均、 はデータの分散。)この式は、
はデータの分散。)この式は、