■　TOP ＞ 応用パソコン統計 ＞ 第12回　 ＞＞＞ NEXT

　▼　第12回　モデルの特定化

■　モデルの特定化

　モデルの特定化はモデル分析における重要な話題であるが、最小二乗法などの推定法とは別の問題として簡単に言及する。

■　一般的な関数型

　すべての関数型がこれまでの例題のような線形で表せられるわけではない。一般的に用いられる関数型とその適用例を列記すると以下のようになる。（a,b,cは、パラメータ）
  1. 一次関数 : Y = a + b X：ケインズ型消費関数
  2. ２次関数 ：Y = a + b X + c X2：平均費用曲線
  3. 双曲線 ： Y = a + b/X：
  4. 片対数型 ： log Y = a + b/X：エンゲル曲線
  5. 両対数型 ： log Y = log a + b log X ：需要関数・供給関数

　□例題12-01：さまざまな関数型 難易度：★★ 目安時間：15分 ノート
　上記の関数型1〜5をX-Yグラフに描くとどのような形状になるかを考える。

■　関数型の選択：モデルの特定化（スペシフィケーション）

　これまでは推定するモデルの型（関数型）が予めわかっていたが、実際には、経済理論（例えば、ケインズの消費関数）に基づいてこれを特定化する。これが線形でない場合もあるので注意を要する。
　□例題12-02：モデルの特定化 難易度：★★ 目安時間：15分 例題集
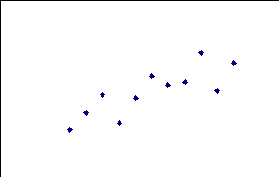
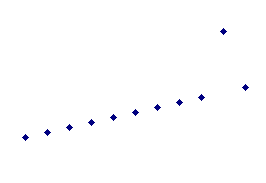
　以下の３つの図(A),(B),(C)には、どのような関数をあてはめたらよいかを考えよ。自分で適当と思われる線（直線・曲線）を図中に赤で書き込みなさい。

　□例題12-03：３種類の関数の推定 難易度：★★ 目安時間：15分 例題集
　上記の各グラフのデータは例題データであるから、それぞれOLSにてY = a + b Xを推定する。推定結果とそのあてはまり具合（決定係数、ｔ値）はそれぞれどうなるか確認する。
これらのデータから得られる最小二乗法の結果（パラメータの推定値）は同じになるはずである。以上のことから式の特定化の重要性を認識してもらいたい。（どのようなあてはめが適当であるかは、[近似曲線]の種類から考えてみよ。）

■　異常値

　データの異常値の取り扱いは最小二乗法などの推定法とは別の問題として簡単に言及する。

　経済データを分析するときには、計測期間に異常値が存在している場合があるので注意をしよう。この異常値のために推定結果が大きく歪められてしまうことがある。この異常値はデータ入力ミスであることもある。異常値を発見するにはグラフ化してみるのが一番よくわかる。異常値が発見できたらその原因を明白にすることは大切であり、重要な情報がそのデータに隠されている場合があるので注意をする。すなわち、その時期に大きく経済構造が変化したようなケースなど、データが生まれてくる背景を調査する必要がある。

　□例題12-04：異常値 難易度：★ 目安時間：5分 例題集
　例題のＣのデータのうち異常値はどれかを示す。

■　ダミー変数

　自由度の項でも述べたが、データは必ず重要な情報を含んでいるので安易に破棄してはいけない。（特に、経済では他の科学とは異なり実験ができないのでデータはより貴重なものとなる。）十分に吟味をする必要がある。

　異常値の対処法としては、ダミー変数（dummy variable）を入れて推定する方法や絶対偏差最小化法などの頑健な推定法などを用いる。

＜ダミー変数法の手順＞
  1. 異常値のある時点設定する。
  2. その時点を１とし、その他の時点は０というような新系列{ 0,0,0,1,0,0,0,0,0 }を作る。
  3. この系列を説明変数に加え重回帰分析を行う。

　□例題12-05：ダミー変数 難易度：★★ 目安時間：15分 例題集
　例題のＣのデータでダミー変数を導入して最小二乗法で推定する。


■　TOP ＞ 応用パソコン統計 ＞ 第13回　

　▼　第13回　総合演習問題

■　消費関数の推定

　マクロ経済学で学習する消費関数を推定する。

　□例題13-01：消費関数の推定 難易度：★★ 目安時間：30分 例題集
　

■　需要予測

　経営データを元に需要を予測する。

　□例題13-02：需要予測 難易度：★★ 目安時間：30分 例題集
　


■ END

last modified :2005.11.05