|
▼ 第04回 ミクロ経済学の例題実習(1)
■ 関数とグラフ
関数の一つの変数に数値を与えることから数値表を作成する。この数値表からグラフを作成することができる。以下では、この方法を学習し、経済学で必要となる関数の描画を行う。
■ 関数の描画
中学校で学習したように、関数(function)はある値xを入れるとそれに対応した値が返ってくるものである。関数をf、入力変数()とし、かえってくるものを出力変数(y)とすると、以下のような式で表すことができる。y = f(x)変数xに適当な値をいれて、その値をもとにyの値を計算する。
Excelでは、以下のような原点となる0から始まる数値表を作ればよい。ここで、f( )は、関数を表す。
| 変数:x |
変数:y |
| 0.0 |
= f(0.0) |
| 1.0 |
= f(1.0) |
| 2.0 |
= f(2.0) |
| 3.0 |
= f(3.0) |
この表の2列をもとにグラフを描くことができる。ここでx列データが横軸、y列データが縦軸になる。
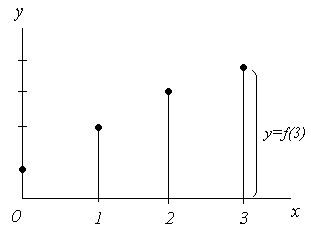
| □例題04-01:関数の描画 |
難易度:★★★ |
目安時間:30分 |
ミクロ |
グラフのもとになる x の範囲(定義域)は0.2きざみで-3 〜 3までとする。yのデータは、以下の標準関数を使い対応する値を計算する。
- 指数関数
- 対数関数
この表を元にグラフを描く。 |
■ 効用関数(1財の場合)
消費者は、財を消費することから満足度を得、その満足度が最大となるように行動することを学習した。いま、リンゴ(x)の消費からえられる効用(U)の関数型(効用関数:utility function)は以下のようであるとする。
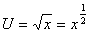
するとデータは、以下の表のように書くことができる。
| リンゴ(数量:x) |
効用(U) |
| 0 |
0 |
| 1 |
1 |
| 2 |
1.414 |
| 3 |
? |
| 4 |
2 |
| 5 |
? |
| 6 |
? |
| 7 |
? |
| 8 |
? |
| □例題04-02:効用曲線の描画 |
難易度:★★ |
目安時間:10分 |
ミクロ |
| 上記の表を完成させ、効用関数のグラフを描く。このグラフの形状からわかることを述べる。 |
■ 費用関数の描画
生産者は、財を生産・販売して得られる利潤が最大となるように行動する。利潤(Profit)は、収入(Revenue)−費用(Cost)で表せることなどミクロ経済学で学習した通りである。ここで、費用と生産量の関係を表す費用関数(cost function)の例題を行なう。
| □例題04-03:費用関数の描画 |
難易度:★★★ |
目安時間:40分 |
例題集 |
例題データの牛の生産業者の生産と費用の表を完成させる。
- この表を完成させ、固定費用を示す。
- 生産量:0〜20頭の範囲この企業の総費用関数を示す。
- 生産量が1〜19頭の範囲で牛1頭あたりの限界費用・平均費用関数を描く。
|
▼ 第05回 ミクロ経済学の例題実習(2)
■ 効用関数(2財の場合)
リンゴ(x)とミカン(y)の消費の組み合わせ(x, y)から得られる効用(U)が次のような式(リンゴの数とミカンの数の積)で表せられるとする。
U = (x,y) = xy
以下の表は、効用を一定(U = 8)とした場合のリンゴ(x)とミカン(y)の組み合わせである。
| リンゴ(数量) |
ミカン(数量) |
効用(U) |
| 1 |
8 |
8 |
| 2 |
4 |
8 |
| 3 |
? |
8 |
| 4 |
2 |
8 |
| 5 |
? |
8 |
| 6 |
? |
8 |
| 7 |
? |
8 |
| 8 |
? |
8 |
■ 無差別曲線
上記の表のように効用を一定とした場合、リンゴとミカンの組み合わせをグラフで表した場合には、双曲線となる。この曲線を無差別曲線(indifference curve)と呼ぶ。
| □例題05-01:無差別曲線の描画 |
難易度:★★ |
目安時間:10分 |
ミクロ |
| 上表を完成させ、無差別曲線を描く。また、効用が4と16のケースの無差別曲線を描く。効用が大きくなると曲線はどのようにシフトするかを考える。 |
|
処理条件:縦軸・横軸の最大値を24に固定する。
|
■ 3Dグラフ
3Dグラフを使うと3次元(3 dimension)の立体図としてグラフを描くことができる。また3Dグラフは、オブジェクトの端+(コーナー)をドラックすることで、さまざまな方向から眺めることができる。
■ 等高線
3Dの等高線は、地図の等高線と同じ概念である。
以下の表では、横軸・縦軸とそのデータの対応が示されている。表のdataが同値ならば、同じ高さとなる。
Excelの表イメージ
| |
Yデータ:横軸 |
X
デ
|
タ
縦
軸 |
data |
data |
data |
data |
data |
data |
data |
data |
data |
| data |
data |
data |
data |
data |
data |
data |
data |
data |
| data |
data |
data |
data |
data |
data |
data |
data |
data |
| □例題05-02:効用曲面の描画 |
難易度:★★★ |
目安時間:40分 |
効用曲面 |
| 3Dグラフの等高線を利用して以下の効用関数の3次元グラフ(効用曲面)を描く。
U = x10.3 x20.3
上の式を利用して、2財(x1 x2)から得られる効用データとグラフを完成させる。完成したらグラフをさまざまな角度から眺めてみる。
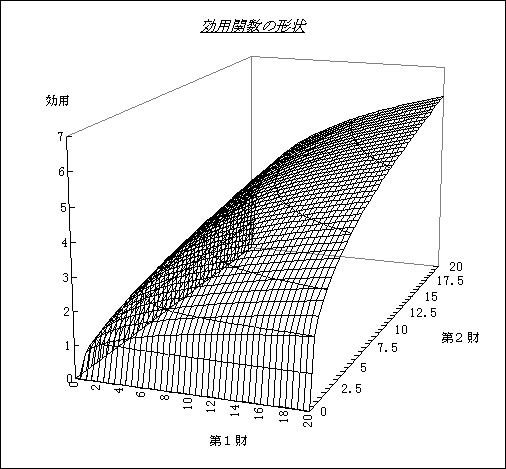
この図が完成後、ワープロにこの図を貼り付け、プリントアウトし、無差別曲線が図中のどの線に対応するかを考える。効用水準が1〜6の無差別曲線を図の中に赤ペンで示し、これを提出する。
|
まず、第A列(縦2〜41)に0から0.5きざみで20までの値(第1財の数)をとり、第1行(横B〜AP)にも同じ幅で値(第2財の数)をとる。関数の式を1つのセル(B2)に書き込み(B2 :=($A2^0.3)*(B$1^0.3)と書く)、それを縦横に1600(40×40)個コピーする。【データの完成】
|
■ コブ・ダグラス型
指数の値の和が1になるような関数型をコブ・ダグラス(Cobb-Douglas)型効用関数という。
| □例題05-03:コブ・ダグラス型効用曲面の描画 |
難易度:★★ |
目安時間:40分 |
効用曲面 |
| 上の例題で作成した効用曲面において指数の値を0.8と0.2とする場合の曲面を描く。例題05-02と比べて、どこが異なるかを考える。
|
last modified :2007.01.05
|


