|
▼ 第04回 残差の概念と残差平方和の計算
■ 残差の概念
データのプロットの例題の結果は全員が同じ答えを得るはずであるが、直線のあてはめの例題では個人によって異なるはずである。個々の主観的判断ではすべての人が納得するような答えは得られない。ある望ましさの客観的基準を決めて、それを満たすような直線を導出すれば、全員が同じ答えを得られるだろう。そこで望ましさの基準を作るため、次のような計算をする。なお、変数下の数字(サブスクリプト)はデータ番号を示す。
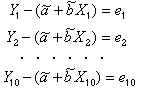 (式04-01) (式04-01)
以上の計算は
現実値−推定値=推定誤差(残差:e)
ということになる。これらの推定誤差eを小さくすることは、推定の誤差が小さくなることなので望ましい基準である。
各推定誤差の和(Σe)は、以下のようなSで表すことができる。
S=e1+e2+e3+e4+e5+e6+e7+e8+e9+e10 (式04-02)
この式の右辺各項の符号は、プラスマイナスまちまちである。
| □例題04-01:残差の計算 |
難易度:★★ |
目安時間:15分 |
例題集 |
|
例題集のデータにおいて残差をExcelで計算する。
|
■作成手順
- aとbを代入するセルを各自で決める。
- aとbを使って、推定値のYの値(=a+bX)を計算する。
- 現実値(Y)から推定値(Y+)を引き、残差(e)を計算する。
- すべてのデータについて以上の計算を行なう。
- (式04-02)は残差の合計。
|
■ 残差平方和
しかし、各eの符号は正と負まちまちであるので、それを統一するため、各eを2乗し符号をプラスにそろえる。推定誤差を平方した値の合計は次のようになる。
S2=e12+e22+e32+e42+e52+e62+e72+e82+e92+e102 (式04-03)
S2=Σei2 (式04-04)
このS2を残差平方和(SSEと呼ぶ)という。これを最小にすることは推定の誤差が最小になることなので、望ましい基準となる。この残差平方和が最小になるようにa,bを決める方法を最小二乗法(Ordinary Least Square Method:略してOLS)という。
注意すべきことは、推定値から離れている現実値(データ)には2乗することにより多くのペナルティを科すということである。
| □例題04-02:残差平方和の計算 |
難易度:★★★★ |
目安時間:10分 |
例題集 |
|
例題集のデータにおいて残差平方和をExcelで計算する。aとbを入力すると自動的に(式04-02)と(式04-04)を計算するようなシートを作る。
|
■作成手順
- 残差を2乗(2乗の計算方法:=(セル番地)^2)して、残差平方を作る。
- すべてのデータについて以上の計算を行なう。
- (式04-04)は、残差平方の合計(残差平方和)。
|
■ 残差平方和の変化
残差平方和は最小となる1点を持つために、aとbを変化させると残差平方和も小さくなる方向がある。これをシートで確認でき、手動で最小値の探索ができる。
| □例題04-03:計算シートでの最小値探索 |
難易度:★★ |
目安時間:10分 |
例題集 |
例題04-02で完成させたシートで以下の問題を行う。
- 計算シートで(式04-02)が0となるaとbの組み合わせを求める。(複数あり)
- 上の条件を満たした状態で、(式04-04)の残差平方和(SSE)が最も小さくなるように各自aとbの値を決める。
- 一番小さくなった結果(aとb、残差平方和)をメモする。
|
|
式04-02は0にならなければならない。Excelのセルで、3.5E-07という表現は指数表現であるので0とみなしてもよい。
|
▼ 第05回 残差平方和の最小値探索
■ 残差平方和を最小にするには
残差平方和を最小にするパラメータaとbを求めるにはどうすればよいか?もちろん残差平方和は平方和であるので、0以上であるが最小値は必ず存在する。まず、残差平方和を簡単な方法で計算してみる。そしてExcelの3Dグラフを利用し、その形状を捉える。
■ 残差平方和の計算(別式)
残差平方和の計算は、以下のような公式でも求められる。(式05-01を展開すればよい)
S2 = Σ(Y - a - bX)2
(式05-01)
S2 = na2 + ΣY2 + b2ΣX2 - 2aΣY-2bΣ(XY) + 2abΣX
(式05-02)
ここで、nはデータ数、ΣX,ΣYはデータX、Yのそれぞれ合計値、ΣX2,ΣY2はXYのそれぞれの平方和、Σ(XY)はXYの積和。
| □例題05-01:統計データの計算 |
難易度:★★ |
目安時間:10分 |
例題集 |
以下の5つの統計量は何と呼ばれるか。また、例題のデータをもとに統計量を計算する。
- ΣX
- ΣY
- ΣX2
- ΣY2
- Σ(XY)
|
| □例題05-02:残差平方和の計算 |
難易度:★★★ |
目安時間:20分 |
例題集 |
|
式05-02を利用し、残差平方和を計算する。この式からaとbの組み合わせと残差平方和の関係を示す。縦軸、横軸には、パラメータa、bをとり、それらの値から残差平方和が計算できるようにする。 |
|
例として、パラメータaは2から0.2刻みで6までとする。bは0.1から0.05刻みで1.00までとする。セルの行と列を固定するには$マークを使う。
|
■ 残差平方和の形状
残差平方和はaとbの二次関数となっている。中学で学習した放物線の形状をもとに3次元(3D)空間でどのように描かれるかを確認する。最も小さい値(底)がただ一つ(ユニークに)存在することを確認する。
| □例題05-03:残差平方和の描画 |
難易度:★ |
目安時間:10分 |
例題集 |
前の例題からaとbの組み合わせと残差平方和を等高線(3Dグラフ)を使って3次元で描画する。なお、縦軸、横軸には、パラメータa、bをとり垂直方向には残差平方和S2をとる。
この図が完成した後、aとbのどの組み合わせが残差平方和を一番小さくするかを観察する。
|
|
垂直方向には残差平方和の値をとるので、グラフの高さが残差平方和である。すなわち効用曲面を作成したときと同じ要領で行う。
|
last modified :2005.11.05
|
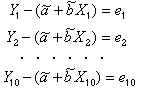 (式04-01)
(式04-01)