|
▼ 第08回 適合度としての決定係数
■ モデルの適合度
残差平方和を最小にする推定量(公式)を導出したあとは、直線(モデル)の当てはまり具合(適合度)を測る客観的尺度を作る。ここでは、全体の説明度合いの尺度として、決定係数を説明する。
| □例題08-01:モデルの適合度 |
難易度:★★ |
目安時間:20分 |
例題集 |
| 例題集のデータにある以下の2つのYデータ(データY1 , データY2 )をもとに散布図を描く。またそれぞれの最小二乗推定値を求めよ。そこから何がわかるかを考える。 |
■ 適合度を測るモノサシ
上記の例題で作成した2つのデータから得られた結果(最小二乗推定値)は同じになる。グラフからもわかるようにデータ1は直線に非常に近いところにデータが散らばっている。反対にデータ2では直線からかけ離れたところに点在している。回帰直線はデータの中心を通るように決めたもので、データとこの直線の適合する程度はデータ1と2では異なる。そこで、推定された直線がデータに対しどれだけの説明力を持っているかという客観的尺度をつくる。
| □例題08-02:残差平方和の比較 |
難易度:★ |
目安時間:10分 |
例題集 |
| 例題集のデータにある以下の2つのYデータ(データY1 , データY2 )の残差平方和を比較する。
|
■ 標本変動と残差
これまでは標本データ(観察値)を用いて回帰直線(モデル)を推定した。この推定された回帰式は、Yの変動部分がある。すなわち異なったXの値に対応するYの観察値がプロットされている。ここで
② 残差( e )= 実際値 - 推定値 = Y - Y* (式08-01)
の大小によって推定された回帰式の適合度が判断されよう。ここでは、推定された回帰式の適合度ないし説明力を判断する基準と手続きを述べる。
まず、Yの標本変動を定義する。何の変動もなければXに対してすべてのYの値は、水平直線の上にある。Yのすべての値が同じであるならば、標本平均値に等しいので、水平線はYaveに対応するものである。さて現実にYの観察値は水平線上のまわりに散布しているので、Yの変動はYの観察値の平均値Yaveからの距離で測られる。
① 偏差y = 実際値 - 平均値 = Y - Yave (式08-02)
次に、回帰直線の変動部分はYの推定値(直線上に点)からYの平均Yaveを引いた値とする。
③ 回帰直線の変動部分 = 推定 - 平均値 = Y* - Yave (式08-03)
これら3つの関係を図示したのが下図である。ここから標本変動(①データの変動部分)と回帰直線の変動部分(③説明されている部分)と残差(②説明できなかった部分)の関係がわかる。
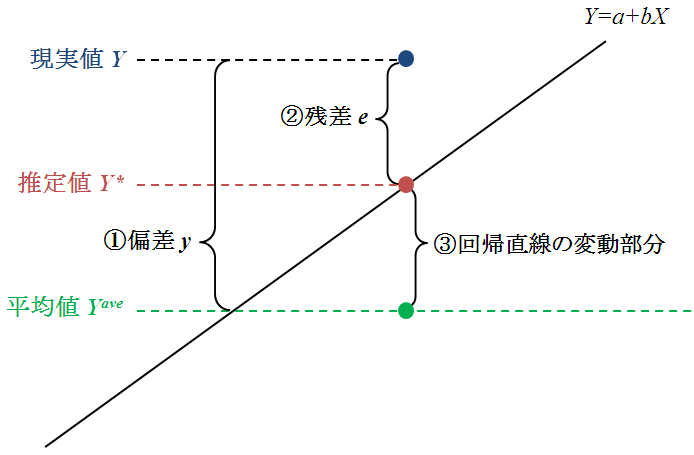
図1. 標本変動と残差
そして、3つの変動について平方和(二乗して全部足したもの)をつくる。
① Yの標本変動(偏差y)の二乗の総和を全変動(Total Sum of Squares:SSTと略す)とすれば、
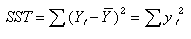 (式08-04) (式08-04)
となる。次に、
② データと推定値の差(残差)の平方和(残差平方和:SSE)は以下のようになる。
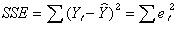 (式08-05) (式08-05)
③ 回帰直線の変動部分の平方和(SSRと略す)は以下のように計算される。
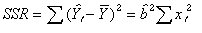 (式08-06) (式08-06)
| □例題08-03:変動部分と残差の部分 |
難易度:★★ |
目安時間:25分 |
例題集 |
例題でプリントアウトした図にX , Yの平均の水平線と垂直線を各軸から引く。平均の交点から気づくことを述べる。
次に図1を参考に、この図を用いて各Yのデータについて標本変動部分(式08-04)を赤ペンで記入する。また、残差の部分(式08-05)を青ペンで記入する。 |
■ 決定係数の導出
全体の変動①に対して、どれだけ回帰直線が説明力を持っているか③という尺度を作るために以下のような割合を定義する。
 (式08-07) (式08-07)
この適合度の尺度「決定係数(Coefficient of Determination )」はSSR/SST(式08-06/式08-04)であり、回帰直線の説明力の割合を示していることになる。決定係数のとりうる範囲は、
0 ≦ R2 ≦ 1
となる。
| □例題08-04:変動部分と決定係数 |
難易度:★★ |
目安時間:15分 |
例題集 |
| 回帰直線の変動部分(式08-06)+ 残差の部分(式08-05)= 全変動(式08-04)を確認する。 |
■ 決定係数の計算ワークシート
決定係数の計算に必要なワークシート部分を例示する。ここでの計算は縦軸の方向Yのみを対象としていることに注意する。また、偏差平方はデータYについての計算であり、すでに計算されているようにyと表現してもよい。
決定係数のワークシート例
| 標本数 |
平均X |
平均Y |
|
a= |
OLS
推定量 |
b= |
OLS
推定量 |
残差合計 |
SSE |
SST |
SSR |
| 10 |
=average |
=average |
|
合計=> |
分子 |
分母 |
|
0 |
② |
① |
③ |
| 標本番号 |
データX |
データY |
偏差x |
偏差y |
積xy |
偏差平方x2 |
推定値:Y* |
残差e |
残差平方e2 |
偏差平方y2 |
回帰直線の変動 |
| 1 |
X1 |
Y1 |
? |
? |
? |
? |
=a+bX1 |
Y*-Y1 |
=e1^2 |
y1^2 |
(Y*-Yave)^2 |
| 2 |
X2 |
Y2
| ? |
? |
? |
? |
=a+bX2 |
Y*-Y2 |
=e2^2 |
y2^2 |
(Y*-Yave)^2 |
| 3 |
X3 |
Y3
| ? |
? |
? |
? |
=a+bX3 |
Y*-Y3 |
=e3^2 |
y3^2 |
(Y*-Yave)^2 |
| 4 |
X4 |
Y4
| ? |
? |
? |
? |
=a+bX4 |
Y*-Y4 |
=e4^2 |
y4^2 |
(Y*-Yave)^2 |
| ... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
| □例題08-05:ワークシートの計算 |
難易度:★★ |
目安時間:25分 |
例題集 |
| 上記ワークシートの例を参考に(赤字のセルを計算する)、これまでの各例題について式08-04、式08-05、式08-06を求める。次に、標本変動を分散から計算して求める。 |
| □例題08-06:決定係数の計算 |
難易度:★ |
目安時間:10分 |
例題集 |
| 式08-07は式0804、式08-05、式08-06でどのように表現されるか。これまでの各例題について式0804、式08-05、式08-06を利用し、決定係数を求める。 |
▼ 第09回 決定係数と自由度による補正
■ 決定係数と相関係数
決定係数は既に学習した相関係数を2乗したものである。1に近いほどその当てはまり具合がよい。(正または負の完全相関を持つ場合に近づく。)しかし、説明変数を増やしてゆくと決定係数は1に近づいてくる。そこで、自由度との関係を考慮した自由度修正済み決定係数もあるので覚えておく。
| □例題09-01:決定係数と相関係数 |
難易度:★ |
目安時間:10分 |
例題集 |
| これまでの各例題の決定係数から相関係数を求める。 |
■ 自由度の概念
1つのデータが持つ情報を1つとすれば、平均を求めた場合、平均からn - 1個のデータを引くと最後の1個のデータは自動的に決定される。このように平均を利用した場合では、データから使用できる情報は1つ少なくなっていることに気づく。一般に回帰分析では、パラメータa,bを推定するのにデータの情報を使ってしまうために、自由度(degree of freedom)はデータ数(n)から推定されるパラメータ数(k)引いたもので決定される。
自由度: n - k (式09-01)
これまでの単回帰の例では、推定されるパラメータは定数項と傾きの係数の2つであったので、n - 2が自由度となる。
| □例題09-02:自由度の計算 |
難易度:★ |
目安時間:10分 |
例題集 |
| これまで学習した例題(
A,
B,
C
)について、その自由度を求める。ワークシートで標本数(n)を自動的に計算するには、どのような関数を用いればよいか。 |
■ 自由度と直線:直観的イメージ
直線を引く場合には、少なくとも2つのデータが必要となる。2つのデータを通る直線を引けば、データと直線のあてはまりはよい。しかし、2つのデータが持つ情報は直線を引くことに利用されてしまっている。3つめのデータからはこの直線の特定するため以外の情報が利用できる。すなわち直線とは関係のない自由なデータとなる。
自由度が低いときには、直線のあてはまり具合は良い。しかし、データから得られる情報が少ないためにモデルの信頼度が低くなってしまうので注意する。また、この自由度はt分布の形状を決定するのに必要となるのでしっかり覚えておこう。
| □例題09-03:データ数と自由度 |
難易度:★ |
目安時間:5分 |
ノート |
|
直線を特定するには、最低いくつの点が必要か。また、面を特定する場合には、最低いくつの点が必要か。
|
■ 自由度0の場合
直線を特定するには最低2つのデータが必要となる。自由度が0の場合は、データが2、パラメータが2である。すなわち直線を特定するためにデータの情報すべてが利用されてしまっている。
| □例題09-04:決定係数が1のケース |
難易度:★ |
目安時間:5分 |
ノート |
|
データが2個でR2は100%であった。この場合の回帰直線とデータの関係を図示する。
|
■ 自由度修正済み決定係数
自由度が低いときには直線のあてはまりはよくなるので、これを割り引いて考えるような決定係数、すなわち自由度で調整した決定係数(自由度修正済み決定係数:
adj R2)を以下のように与える。
adj R2=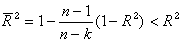 (式09-02) (式09-02)
(ここで、n:データ数、k:説明変数の数)
式にもあるように自由度修正済み決定係数は決定係数よりも小さい値をとることに注意する。(証明略)
| □例題09-05:自由度修正済み決定係数の計算 |
難易度:★★ |
目安時間:15分 |
例題集 |
| これまで学習した例題(
A,
B,
C
)について、その自由度修正済み決定係数を求める。 |
last modified :2005.11.05
|

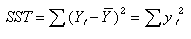 (式08-04)
(式08-04)
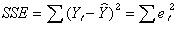 (式08-05)
(式08-05)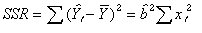 (式08-06)
(式08-06)
 (式08-07)
(式08-07)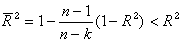 (式09-02)
(式09-02)