|
▼ 第12回 2変数の関係(1)
■ 変数間の関係
これまで1変数のデータの特徴について学習した。その内容は、データの代表値として平均、散らばりの尺度として分散などを表計算ソフトで計算した。次のステップでは、データ同士の相互関係、2変数の関係を調査する。経済学においてはデータ同士の関係(例えば、所得と消費の関係や気温とビールの販売量の関係など)を調査することが重要となるので、これらの関係の分析方法を学習する。
この方法として相関分析と回帰分析という考え方がある。相関は、2変数XとYの間に区別をしないで関係の度合いを測定する方法である。一方、回帰は、変数の間に因果関係があるとみなし、XはYをどれだけ説明しているか、YはXにどのように決定されるかを判断する。
| □例題12-01:散布図 |
難易度:★★ |
目安時間:20分 |
例題集 |
|
例題集のデータから散布図を作成する。折れ線グラフとはどこが異なるかを考える。 |
■ 散布図
2組のデータの関係を調べるためには、まず、データをグラフ化して観察することが最も簡単な方法である。XとYという2組のデータを横軸と縦軸にとってグラフにするとその関係がわかる。これを散布図( Scatter Diagram :プロット図)という。
散布図を描くには、グラフウィザードの散布図を選択する。確認すべき基礎事項としては、横軸と縦軸の項目がそれぞれXとYというように数値軸になっているかどうかである。
| □例題12-02:散布図と平均 |
難易度:★★ |
目安時間:20分 |
例題集 |
例題集の2つのデータを使い以下の統計量を求める。(1)平均、(2)分散、(3)標準偏差
また、XとYの平均値を図中に示す。
|
■ 偏差の積
XとYのそれぞれの偏差を掛け算したものは以下の式で表現できる。
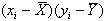 (式12-1) (式12-1)
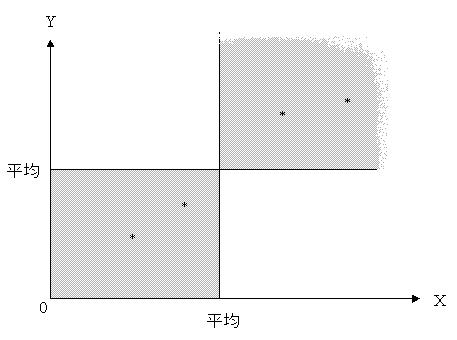
この式の結果を見れば、XとYが共に平均よりも大きい場合とXとYが共に平均よりも小さい場合にはグレーの領域に分布する。この関係を利用すれば、XとYの関係を表現できる。
| □例題12-03:偏差の積と和 |
難易度:★★ |
目安時間:20分 |
例題集 |
| 例題集のデータからXとY偏差の積をすべて計算する。それをすべて合計する。 |
▼ 第13回 2変数の関係(2)
■ 相関係数
散布図を眺めるだけでなく、実際どれほど直線的な関係があるのかを数量的に示す必要がある。そこでXとYの2変数の相関係数 ( Correlation Coefficient )を以下に定義する。
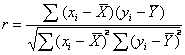 (式13-1) (式13-1)
煩雑な式であるが、この式で平均偏差が利用されていることに注意する。
また、分母には平方根がついており必ず正の値となるので、分子である偏差の積和がこの係数rの符号を決定する。この式から相関係数は1から−1の値とることがわかる。
-1 ≦ r ≦ 1
次の条件では、以下のように判断する。
0 < r :正の相関, r < 0 : 負の相関
r = 0 :無相関, r = ±1 : 完全相関
完全相関の場合には、データが一直線上に並ぶ。
| □例題13-01:相関係数 |
難易度:★★ |
目安時間:10分 |
ノート |
式13-1の分子に利用されている各偏差(Xの偏差とYの偏差)は、上の図の横軸と縦軸ではどこに相当するかを確認する。
分子の各データ(Xの偏差とYの偏差の積)が、グラフの中で正と負の値をとる範囲をそれぞれ示す。
|
■ 共分散
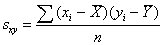 (式13-2) (式13-2)
式2より分散と共分散( Covariance )はどこが異なるのかを確認する。また、相関係数とはどこが異なっているかを考察する。
| □例題13-02:相関係数と共分散 |
難易度:★★ |
目安時間:20分 |
例題集 |
|
例題集のデータの相関係数と共分散を標準関数と式13-1、13-2の公式を使って求める。このXとYのデータにはどのような関係があるかを相関係数から判断する。 |
| □例題13-03:相関係数と共分散 |
難易度:★★ |
目安時間:20分 |
例題集 |
例題集のデータは東京都区部における1994年1月から8月までの月平均気温(単位:℃,X)と、一世帯当たりのビールの消費量(単位:リットル,Y)である。これらのデータを使い以下の統計量を求める。またプロット図を作り各統計値とその関係を比較してみる。ビールの消費量と気温にはどのような関係があるのかを確認する。
(1) 平均 (2) 分散 (3) 標準偏差 (4) 相関係数 (5) 共分散 |
■ 決定係数
相関係数を二乗したものが決定係数(Coefficient of Determination :R2)である。これは応用パソコン統計で学習する回帰分析において解説をする。
R2= r2 (式13-3)
| □例題13-04:決定係数 |
難易度:★★ |
目安時間:10分 |
例題集 |
|
例題のデータについて決定係数を標準関数と相関係数からそれぞれ求める。 |
■ 相関分析と回帰分析
XとYのそれぞれの偏差を散布図の中で記入する。
この方法として相関分析と回帰分析という考え方がある。相関は、2変数XとYの間に区別をしないで関係の度合いを測定する方法である。一方、回帰は、変数の間に因果関係があるとみなし、XはYをどれだけ説明しているか、YはXにどのように決定されるかを判断する。
■ 統計的処理(2)
経済データを分析するうえで必要となる統計学の内容を、実際に表計算ソフトのワークシート上で計算をしながら確認してきた。しかし、これまでは母集団と標本という区別をせずに統計量を計算してきた。ここまでの学習内容は記述統計と呼ぶ。
記述統計では、与えられたデータについてのさまざまな特性(散らばり、分布など)を調査・整理することを目的とする。経済学におけるデータ分析で必要となるのは推測統計という考え方である。ここでは、実際の母集団から得られたデータ(標本)に基づいて母集団の特徴を推測することを行う。これらの取り扱いには不確実な要素(確率)が含まれることに注意し、特に、確率分布や確率変数などの内容については参考書などで知識の確認をしてもらいたい。
今後のさらに進んだ学習課題として、推測統計の考え方、特に母集団と標本の考え方をマスターしなければならない。そして、標本から母集団を統計量(平均や標準偏差)を推定する考え方・方法を学ぶ。代表的推定法として最小二乗推定法の仕組みを計算しながら学習するのが一般的であろう。次に、推定された値が母集団から得られた標本であるかをチェック(テスト)するために統計的検定を学習する。
■ END
last modified :2007.01.05
|

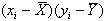 (式12-1)
(式12-1)
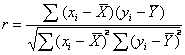 (式13-1)
(式13-1)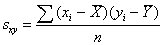 (式13-2)
(式13-2)