|
▼ 第10回 散らばりの尺度(1)
■ データの散らばり
データの代表値としてさまざまな代表値を導いた。次にデータの散らばり具合(尺度)を示す指標を作成する。この指標には、レンジほか分散や標準偏差・変動係数などがある。
■ レンジ
データの平均とは関係なく散らばりの範囲を与えるものとしてレンジ(range)がある。最大値と最小値の差をレンジとする。
レンジ=MAX(範囲) - MIN(範囲) (式10-1)
レンジは、全データ(n )のうちで2つのデータしか使っていない。すなわち残りのデータ( n -2 個)の持つ情報は使っていない。レンジの問題点としては、外れ値(一つだけとんでもなく異なった値のデータ)の影響を受けやすいことが挙げられる。データが大きくなるに従い、レンジも大きくなる傾向があるので注意する。
| □例題10-01:レンジと外れ値 |
難易度:★ |
目安時間:10分 |
ノート |
| 16家族の子供の数が 0,0,0,1,1,1,2,2,2,2,2,3,3,3,4,7である時のレンジを求める。この場合、7人の子供を持つ家族のデータが、どのように影響するかを考察する。 |
| この例題はExcelを用いず、ノートで行う。 |
■ 四分位範囲
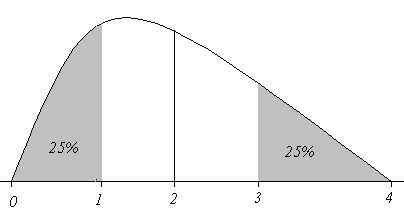
レンジの問題点を補正するものとして、四分位範囲( interquartile range)がある。これはデータを大きい順番に並べ四分割する(各25%)し、上位25%の点(第1四分位)と75%の点(第3四分位)の範囲を四分位範囲とする。以下のように示される。
四分位範囲 = 第3四分位 − 第1四分位 (式10-2)
Excelの標準関数を使った計算は、=QUARTILE(データ , 3) - QUARTILE(データ
, 1)となる。ここで戻り値は0〜4であり、それぞれ図中の数値を表示する。
- 0: 最小値
- 1: 第1四分位
- 2: 第2四分位(中位数:メジアン)
- 3: 第3四分位
- 4: 最大値
| □例題10-02:範囲の長さ |
難易度:★ |
目安時間:5分 |
ノート |
| 上図でレンジ・四分位範囲の長さを赤ペンで示す。 |
レンジと四分位範囲の関係は、上の図で灰色の部分を含めた範囲とそれらを除いた範囲の違いである。
データが正規分布となっていない場合や外れ値(異常値)がある場合などに対して有効である。レンジと同様に四分位範囲はすべてのデータのうち2つしか利用していない。(データが持っている情報が十分利用されていない)
| □例題10-03:四分位範囲 |
難易度:★★ |
目安時間:15分 |
例題集 |
| 例題集のデータからレンジ・四分位範囲をそれぞれ求める。 |
■ 分散
分散( variance )定義:データから平均値の差(平均偏差:deviation )を2乗したものの平均値
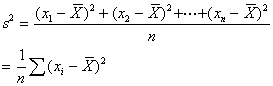 (式10-3) (式10-3)
分子に用いられている偏差は、平均からの距離であり、平均より小さいデータは負、平均より上のそれは正の符号になる。また平均と同じ値のデータはゼロになる。(平均偏差の概念)この偏差を2乗したもの(符号はすべて正となる)の合計を偏差平方和と呼ぶ。分散は、偏差平方和をデータ個数(n )倍で割ったものである。
分散は遠くに離れているデータに対しては、二乗することからより大きなペナルティを科していることに注意する。分散はすべてのデータの持つ情報を利用しているので、外れ値の影響を受けやすい。
| □例題10-04:分散 |
難易度:★★ |
目安時間:10分 |
例題集 |
| 例題集のデータを元に分散を標準関数と公式の両方で計算する。 |
■ 標準偏差
標準偏差( standard deviation )定義:分散の平方根
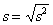 (式10-4) (式10-4)
2乗計算から得られた分散に対してルートをとれば、元のデータと同じ次元に戻る(面積と長さの関係を想起せよ)。同じ次元であるからデータとの比較が可能なので大変よく用いられる。
データが正規分布(■正規分布の図を参照)に従うと仮定した場合には、標準偏差とデータの含まれる割合は以下のような関係がある。
平均 ± s 68.3%
平均 ± 2s 95.4%
平均 ± 3s 99.7%
| □例題10-05:標準偏差 |
難易度:★★ |
目安時間:30分 |
例題集 |
| 例題集のデータを元に標準偏差を標準関数と公式の両方で計算する。 |
■ 度数分布表と分散・標準偏差
級の幅が1の場合には、度数分布表から分散・標準偏差を計算することができる。計算方法は、以下の通り。
- 平均値を導出する。
- 平均からの偏差をとる。
- 平均偏差を2乗する。
- 偏差平方を合計する。【偏差平方和】
- 偏差平方和をデータ数で割る。
| □例題10-06:度数分布表 |
難易度:★★★ |
目安時間:30分 |
例題集 |
| 例題集のデータから分散と標準偏差を計算する。
【関連】例題9-3
|
▼ 第11回 散らばりの尺度(2)
■ 偏差の考え方
偏差とはある基準からの差のことであり、相対化した値でもある。通常、平均を基準として偏差をとる(平均偏差)。
偏差の計算: 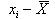 (式11-1) (式11-1)
この値の符号によって、平均以上かどうかが判定できる。マイナスの値であれば、平均以下であることを示す。
| □例題11-01:偏差 |
難易度:★★ |
目安時間:10分 |
例題集 |
| 例題集のデータから50人の生徒ひとりひとりの偏差を計算する。 |
■ 偏差値
受験生には、馴染みのある偏差値について解説する。これは基準化と同じ考え方である。同じ受験生(母集団は同じ)の受験科目の成績を比較するとき、国語は平均点55点、数学は平均点70点とする。ここである受験生が国語は70点、数学は90点とったとすると彼はこの受験生の中でどれぐらいの成績を取ったことになるか?
偏差値は以下のような計算から求まる。
偏差値の計算: 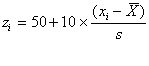 (式11-2) (式11-2)
位置の尺度としての平均と散らばりの尺度としての標準偏差を用いており、平均を50点、標準偏差を10点とするモノサシである。偏差値では、成績が1番でも飛び抜けた1番かどうかも判断できる。最高点がともに95点であり、それぞれの偏差値が70、75であった場合に、後者の科目の方が他の受験生の平均的能力に比較してより優れていると判断ができる。
しかし、母集団が異なると偏差値の比較は意味のないものになる。なぜならば、優秀な学生の中での偏差値55と、そうでない集団での偏差値60ではどちらが優れているのかという判断はできないからである。
| □例題11-02:偏差値 |
難易度:★★★ |
目安時間:20分 |
例題集 |
| 例題集のデータから50人の生徒ひとりひとりの偏差値を計算する。 |
■ 分布
データの状態を示しているのが、分布( Distribution )である。これまでヒストグラムで描かれたデータの形状が分布状態を示している。全体の特徴をグラフにより直観的に捉えた後、分布を構成しているデータの中心がどのような位置にあるのか、データの散らばりの程度について数値として表すことを今後学習する。
| □例題11-03:分布の種類 |
難易度:★ |
目安時間:10分 |
ノート |
| どのような分布があるか。統計学のテキストを参考に3つ以上列記する。 |
■ 正規分布
連続的確率分布として正規分布( Normal Distribution )を挙げておく。よく知られているように、これは平均を中心として左右対称の釣り鐘状の形をしているので、平均に近い値が出る確率が高く、平均からかなり離れた事象はあまり起こらない。分散(標準偏差)の大きさによりその形状が変化する。(散らばりが大きければ裾野が広くなる。)
いろいろな現象に応用され、また正規分布から他の分布(カイ二乗分布、t分布、F分布)が導かれるので、最も重要な分布である。Excelの標準統計関数にもこの分布についての各種統計量の関数があるので参照されたい。この分布は推測統計において、区間推定や検定に利用する。
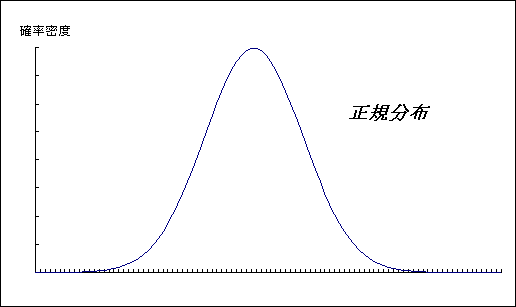
図11-1 正規分布の形状図
| □例題11-04:正規分布と平均 |
難易度:★ |
目安時間:3分 |
ノート |
| 上図の分布で平均の位置を示す。 |
■ 正規分布の描画
正規分布の形状を描画するには以下の2つの方法がある。
- 公式による方法
- 正規分布の累積密度関数を使う方法
■ 正規分布の公式
正規分布の公式から正規分布の図を描画する。 平均μ、分散σ2であるような確率密度関数:
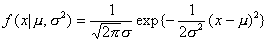 (式11-3) (式11-3)
平均は位置の尺度であるから、これを変化させると中心の位置が左右にずれる。散らばりの尺度である標準偏差を変えた場合には、幅は狭く(山が高く)なることがわかる。
表11-1 確率密度関数
| x |
式の右辺 f(x) |
| -4.6 |
=EXP(-(X^2)/2)/SQRT(2*PI()) |
| -4.5 |
... |
| -4.4 |
... |
| ... |
... |
| ... |
... |
| ... |
... |
| 4.5 |
... |
| 4.6 |
... |
| 4.7 |
... |
| □例題11-05:正規分布の描画 |
難易度:★★★ |
目安時間:30分 |
分布 |
| 上記の方法で正規分布を描く。■関数の描画と同様の方法である。まず最初に、分散σ2=1、平均μ=0の場合の描画する。この場合には式8はどのようなるかを考える。つづいて、分散と平均を変化できるワークシートを作成する。この場合、式2のσとμを変化させ、その形状を観察できるようにする。 |
■ 正規分布の累積密度関数
正規分布の累積密度関数を使って描画できる。使用する標準関数は、以下の2つである。
表11-2 正規分布の密度(度数)分布
| 範囲 |
累積密度 |
| -4.6 |
=1-NORMDIST(ABS(セル<),0,1,true) |
| -4.5 |
=1-NORMDIST(ABS(セル<),0,1,true) |
| -4.4 |
=1-NORMDIST(ABS(セル<),0,1,true) |
| ... |
... |
| ... |
... |
| ... |
... |
| 4.5 |
=1-NORMDIST(ABS(セル<),0,1,true) |
| 4.6 |
=1-NORMDIST(ABS(セル<),0,1,true) |
| 4.7 |
=1-NORMDIST(ABS(セル<),0,1,true) |
| □例題11-06:正規分布の描画 |
難易度:★★★ |
目安時間:25分 |
分布 |
| 上記の方法(上記の度数分布表を作成し)で正規分布(折れ線のヒストグラム)を描く。なお、分散は1、平均は0(標準正規分布)とする。 |
■ 統計学の意味
これまで行ってきた計算は、すべてデータが持つ情報を公式を使って計算し数値化することであった。これら計算の公式(統計量と呼ぶ)は、データの特徴を知る上でさまざまな判断の助けとなる。統計学とは、利用可能な情報を加工・整理し、意志決定に役立てる学問である。
| □例題11-07:分析ツール(基本統計量) |
難易度:★★ |
目安時間:20分 |
分布 |
| 分析ツールの中には、基本統計量という項目がある。データを元に基本統計量を導出してみる。どのような統計量が出力されるか確認する。 |
last modified :2007.01.05
|



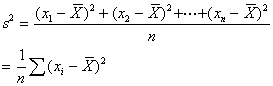 (式10-3)
(式10-3)
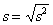 (式10-4)
(式10-4)
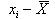 (式11-1)
(式11-1)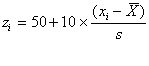 (式11-2)
(式11-2)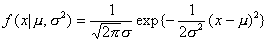 (式11-3)
(式11-3)