|
▼ 第08回 データの代表値と変化率(1)
■ 統計的処理
経済分析に必要な基本統計量を実際に計算しながら確認してゆく。データ(標本)の特徴を客観的な尺度を用いて把握する。なお、例題で経済データを使用する場合には、各データ背景も併せて学習してもらいたい。
■ データの代表値
多くのデータのなかでそれらを代表する値としては、モード(最頻値)、メジアン(中央値)等の他に平均などがある。この3つ代表値の特徴や計算方法を説明する。
■ モード
モード(mode,最頻値)定義 : 度数分布表において最大の度数を持つ階級値値が同じデータの個数を数えたとき、最も個数の多いデータの値を“最頻値(モード)”という.ただし,値が同じデータの個数が1や2と少ないときは意味のないものである。
■ メジアン
メジアン(median, 中央値:中位数)
定義 : データを小さい順に並べていったとき中央になるデータの値 データをその値の小さい順ないし大きい順に並べたとき,真ん中の順位にくるデータの値を“中位数(メディアン)”という.データの個数が奇数のときは真ん中の順位が存在するが,偶数のときは真ん中に相当する順位が存在しないので,中央の順位にくる2個の値の平均値をもって中位数とする.
データ数(n )が偶数の場合には、中心となる2つのデータの平均とする。
| □例題08-01:モード・メジアン |
難易度:★ |
目安時間:10分 |
例題集 |
| 例題集にある表のデータのExcelでモード、メジアンを求める。 |
■ 算術平均
算術平均( arithmetic mean )定義 : 通常使っている平均。全データの合計をデータ個数(n)で割る。
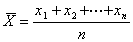 (式8-1) (式8-1)
| □例題08-02:平均 |
難易度:★ |
目安時間:5分 |
例題集 |
| Excelで例題(50人のテスト結果)の平均を求める。 |
平均の特徴:
- あるデータから平均をひいた値(平均偏差)をすべてのデータについて足しあわせるとゼロになる。
- データを確率変数とすれば、その期待値というのは平均となる。(度数分布表の重心)
- 偏差の2乗和が最小となる値
| □例題08-03:分布と代表値 |
難易度:★★ |
目安時間:5分 |
ノート |
以下の図中にある(1)(2)(3)の位置は、これまで説明した3つの代表値のいずれになるか?
この場合、(3)の左半分の面積と右半分のそれは等しいものとする。
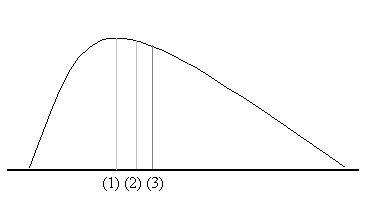
【関連】例題8-5
|
| 正の歪みがある分布は上記のようになる。
|
| □例題08-04:分布と代表値 |
難易度:★★ |
目安時間:5分 |
例題集 |
|
50人の成績がデータのように求められたとする。この科目の度数分布表を階級数を20として作成し、ヒストグラムを描く。また、最高点と最低点を示した後、これらのデータからモード、メジアン、算術平均をそれぞれ求める。その3つの代表値の大きさを比較し、そこから何がいえるかを考察する。(ヒストグラムより分布状態を把握する。)
|
| □例題08-05:平均と経済データ |
難易度:★★ |
目安時間:5分 |
ノート |
以下の表は1世帯当たりの貯蓄である。家計の平均収入や貯蓄がわれわれの感覚とかけ離れて大きいと感じるのは何故だろうか?このような場合、平均の代わりにどのような指標を用いたらよいかを考える。(これらのデータのヒストグラムはどのような形状をしているかを想起する。)
表 1世帯当たりの貯蓄
| 年度 |
所得 |
貯蓄 |
| 平成4年度 |
750万円 |
1,536万円 |
| 平成5年度 |
751万円 |
1,498万円 |
(総務省統計局「貯蓄動向調査報告」より)
|
▼ 第09回 データの代表値と変化率(2)
■ 加重算術平均
通常の平均は、すべてのデータを均一のものとして扱っている。しかしデータの中には重要なものがあり、この重要度をデータ反映するためには、重みを付けて平均を取る方法がある。例えば、主要5教科で英語を重視するならば、他の科目よりも英語に相当の重みを付ければよい。
加重算術平均( weighted arithmetic mean )定義 : データの重要度に応じたウェイト( w )をそれぞれのデータに与えて平均を計算する。
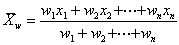 (式9-1) (式9-1)
| □例題09-01:加重平均 |
難易度:★★ |
目安時間:10分 |
平均 |
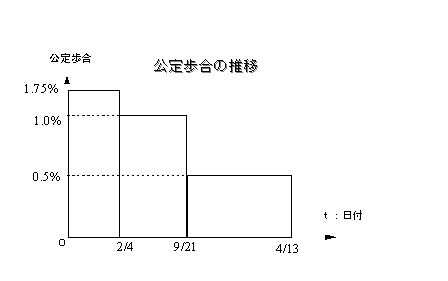
下記の1993年〜1995年の公定歩合の各平均を求める。
- 公定歩合の算術平均
- 公定歩合の加重算術平均
表9-1 公定歩合の推移
| 公定歩合 |
期間 |
| 3.25 % |
93/1/ 1 〜 93/ 2/ 3 |
| 2.50 % |
93/2/ 4 〜 93/ 9/20 |
| 1.75 % |
93/ 9/21 〜 95/ 4/13 |
| 1.00 % |
95/ 4/14 〜 95/ 9/ 7 |
| 0.50 % |
95/ 9/ 8 〜 95/12/31 |
(資料:日本銀行「経済統計月報」)
|
Hint! (2)は、各公定歩合の実施期間を計算し、その日数をウェイト( w )として計算する。
また、表示がおかしな場合には、セルの表示を日付や数値に変える(Excelの基礎を参照)。
|
■ 幾何平均
幾何平均( geometric mean )定義 : n 個のデータの積のn 乗根
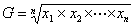 (式9-2) (式9-2)
増加(変化)率(変化率・成長率を参照)の平均を用いるのに使うことがよいとされる。経済学でよく用いられる対前年比増加率(経済成長率・賃金増加率)などを計算する場合には、算術平均でなくこれを使う。ただし、データの中に一つでも0があると幾何平均は0になってしまうので注意する。
| □例題09-02:変化率の平均 |
難易度:★★ |
目安時間:20分 |
例題集 |
例題のGDEの対前年比の増加率(成長率)の平均を求める。各年の成長率は、■変化率(成長率)のdではなく、以下の計算で求めたものとする。(何故か?)
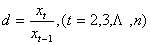 (式9-3) (式9-3)
【関連】例題3-2
|
■ 度数分布表と平均
テストなどのデータで級の幅が1の場合には、度数分布表から平均値などを計算することができる。
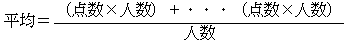 (式9-4) (式9-4)
| □例題09-03:度数分布表 |
難易度:★★ |
目安時間:10分 |
例題集 |
|
例題データより最高点・最低点を示し、受験者数と平均点を計算する。また、メジアン・モードはいくつになるかを求める。
【関連】例題10-6
|
last modified :2007.01.05
|

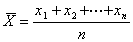 (式8-1)
(式8-1)

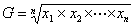 (式9-2)
(式9-2)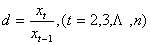 (式9-3)
(式9-3)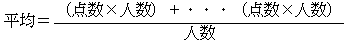 (式9-4)
(式9-4)