|
▼ 第02回 散布図の作成:回帰分析
■ 回帰分析
経済分析において最もよく用いられるのが回帰分析(regression analysis)である。変数の間に何らかの因果関係があるものとして関係を数式で特定し、実際にデータを当てはめることからその関係を評価する(相関分析とはどこが異なるかを考えよ)。このように、回帰分析とはある与えられた変数(被説明変数)と1つ以上の変数(説明変数)との間の因果関係を調査する方法である。被説明変数は従属変数、説明変数は独立変数とも言われる。説明変数が一つの場合を単(純)回帰といい、2個以上の場合を(多)重回帰という。
なお、この講義では重回帰は扱われない。
■ 関係の特定化:確率モデルと確定モデル
以下のような単回帰モデルを特定する。
Y = a + b X (式02-01)
ここで、Xは説明変数、Yは被説明変数である。実際のデータは式02-01と厳密に一致しないので、この式に誤差項uを加える。式02-02は確率的要素を含んでいるので確率モデルと呼ばれる。
Y = a + b X + u (式02-02)
ここで、誤差項には、
- 予測不可能な要素
- 他の変数の影響
- 測定誤差
などが含まれている。以下では、式02-02の確率モデルを前提にデータ間の関係を捉える。
■ 誤差項uに関する仮定
誤差項には以下のような望ましい(都合の良い)仮定をおく。現実にはこのような仮定が保証されない場合が多く、非常に厳しい仮定である。後にこれらの仮定が満たされない場合について一つずつ検証・学習してゆく。
- 分散一定
- 平均が0
- 誤差項は互いに無相関
- 説明変数と誤差項は互いに無相関
- 正規分布
以上の性質を記号で書くならば、u〜N(0,σ2)となる。ただし、条件5.については検定の際に必要となる。
■ 推定方法
推定の基本的考え方を利用して変数の関係を捉える。実際のデータを用いて特定化された変数間の関係を評価する推定方法は、積率法、最小二乗法、最尤法(さいゆうほう:Maximum Likelihood Method)などがある。
■ 最小二乗推定法
実際のデータを利用して現実のシステム(関数)を推定する方法として最小二乗法(Ordinary Least Square Method:OLSと略す)を学習する。この方法は扱いが簡単で、最もよく使われており、いずれの計量経済学や統計学のテキストにも載っているので参考にして欲しい。まずは、2変数の関係の場合として単回帰の最小二乗推定法について学習する。
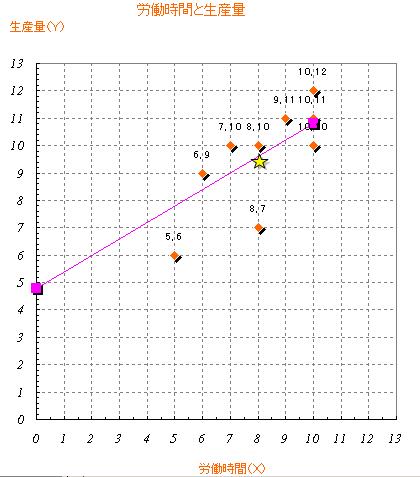
■ 2つのデータの関係(散布図)
次の例題を用いて最小二乗法の仕組みを表計算ソフトを用いて説明する。実際に関数を推定する際にもこのような方法で行えばよい。まず、スプレッドシートにデータの系列を入力し、入力ミスなどがないかグラフ化して確認する。
| □例題02-01:散布図 |
難易度:★ |
目安時間:20分 |
例題集 |
|
例題集のXとYのデータから散布図をシートに作成する。編集ポイントに注意してシート名は「労働と生産量」。ヘッダーフッターに自分の学籍番号と名前を入れて印刷する。 |
|
【編集ポイント】Excelのグラフの復習。完成したグラフはできるだけ見栄えの良いものとする。目盛りや補助線などをつけ方眼紙のようにする。
|
■ 中心を通る直線
散布図に中心を通るであろうと思われる直線を描くことができる。その直線の式は以下のようになる。
Y = a + b X (式02-03)
ここでaは直線のY切片、bは傾きである。
| □例題02-02:図形の追加(平均値と直線) |
難易度:★ |
目安時間:10分 |
例題集 |
|
例題集のXとYの各平均値(X , Y)を計算し、散布図に☆マークをつける。また、データの中心を通ると思う直線を記入する。 |
|
Excelの図形描画バーを利用し、☆マークと直線を図中に貼り付ける。なお、直線はY切片と交差すること。
|
▼ 第03回 データへの直線のあてはめ
■ 変数間の関係
例題の散布図をみるとX,Yに何らかの関係があると思われる。この関係を特定化する。いま
- Y = a + b X (式03-01)
という線形(一次)関係があると仮定すれば、散布図の中に切片aで傾きbをもつ直線が引けるはずである。
| □例題03-01:直線の切片aと傾きbの導出 |
難易度:★ |
目安時間:10分 |
例題集 |
|
例題データから作成した散布図で、各自で引いた直線のa、bを調査する。
|
直線の切片aは、縦軸との交点で測る。(補助目盛りをつけるとわかりやすい)
直線の傾きbの導出の仕方は、 Yの増加量/Xの増加量である。Xの増加量を10としたときに、Yがどれだけ増加したのを調査する。
|
■ Excelのグラフの利用:系列の追加
作成手順は以下の通り。
- 切片と傾きのセルを作る。(切片aと傾きbの値を変えると再計算されることを確認)
- 直線の端点2つを計算するセルを作成する。(Y切片の値とXが最大のYの値)
- グラフをアクティブにする。
- グラフウィザードの2/4で系列の追加をする。
- 新しい系列をダブルクリックして、パターンの線を指定する。
- 切片aと傾きbの値を変化させ、直線が動くかどうかを確認する。
| □例題03-02:直線の追加 |
難易度:★★ |
目安時間:25分 |
例題集 |
|
例題データより各自で求めた切片aと傾きbのセルを作成する。そのセルを元に新しい系列をグラフ表示し、直線を引く。
|
|
■データ系列の追加
|
last modified :2005.11.05
|